Let's color
2 participants
Page 1 sur 1
 Let's color
Let's color
Bonjour chers-chère lecteur-lectrice.
Aujourd'hui j'aimerais te parler de coloriage !
Parce que le coloriage, c'est la vie.
Sauf qu'aujourd'hui tu n'auras que 2 couleurs : rouge et bleu.
On va placer plein de points et on va s'amuser à tous les relier entre eux, avec du rouge ou du bleu.
Alors munis-toi d'une feuille et de deux stylos/crayons de couleurs et let's color !!!
Comme ceci par exemple :

On va peut-être prendre plus de points, genre 5.
Et on va les relier entre eux :
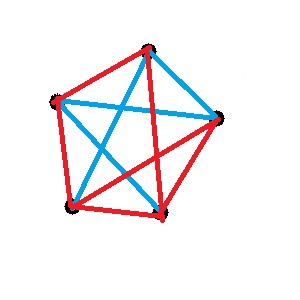
Rien de très stimulant intellectuellement, pour l'instant du moins ... ;-)
Alors je te propose un petit casse-tête, quelque chose de simple t'inquiète.
Essaie de relier les 5 points entre eux, en utilisant les deux couleurs, pour qu'aucun triangles ne soit unicolore.
En gros il ne doit pas y avoir de triangles uniquement rouges, ou uniquement bleus.
L'exemple que j'ai donné plus haut ne fonctionne pas, le triangle en bas à droite est complètement rouge.
Ha au fait petit malin, je parle des triangles dont les sommets sont des points noirs, pas des triangles formés par les intersections des traits.
Celui-ci oui :
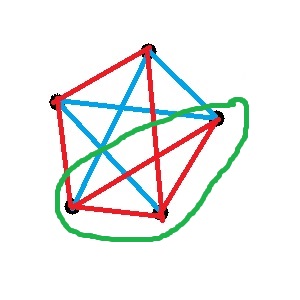
Celui-ci non :
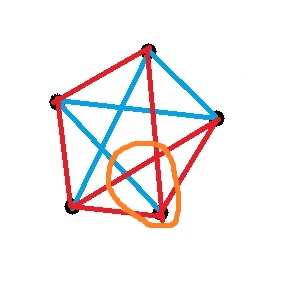
Si tu n'arrives pas à trouver la réponse, la voici :
Avant d'aller plus loin j'aimerais introduire ici quelques termes.
Non !!! Ne pars pas !!! C'est pas compliqué promis !
Si tu es encore là, déjà merci et bravo, ensuite voici les termes : "Graphes complets".
Qu'est-ce qu'un graphe ? Et bien en math c'est rien de plus que des points et des traits qui relient les points, appelées arêtes.
Il y a une définition plus précise ICI.
Et un graphe complet, et bien c'est juste un graphe où tout les points sont reliés entre eux.
Tu vois que c'était pas dur !
Un petit dernier pour la route : "sous-graphe".
Un sous-graphe d'un graphe G, c'est juste un graphe contenue dans G.
Pas trop mal à la tête ?
Alors pour dire la même chose que plus haut mais avec le bon vocabulaire :
On a un graphe complet de taille 5 (5=le nombre de sommets), appelons-le G (comme Graphe XD vive l'originalité ...)
Et on cherche à colorier chaque arêtes de telle sorte que tout les sous-graphes de taille 3 ne soient pas unicolores.
Prends le temps de digérer cette phrase ;-).
Alors on continue.
Imagine maintenant qu'il y a 6 points à relier.

Et là, même question. Colorie le graphe complet, de taille 6, pour que chaque graphe de taille 3 contenu dedans ne soit pas unicolore.
Ne regarde pas la suite et réfléchis un peu ;-)
Alors ?
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Et bien la solution est simple : il n'y en a pas.
Et oui ce n'est pas possible !
Et je m'en vais te le prouver ! (parce que l'on fais quand même un peu de math XD)
Mais sans faire de calcul ! (parce que l'on fais quand même un peu de dessins XD)
Pour pas se répéter indéfiniment, on dira qu'un graphe G qui peut être colorié (de telle manière à ce que tout sous-graphe de taille 3 ne soit pas unicolore) vérifie la propriété P3.
D'abord, petit Lemme (un lemme c'est un théorème intermédiaire utile pour prouver un autre résultats).
"Si un Graphe vérifie P3, alors de chaque sommets, il ne peut pas partir plus de 2 arêtes de la même couleur."
Alors pourquoi ?
Et bien dessinons.
Si je prends un point et que je trace plus de 2 traits de la même couleur. Plus de 2, donc on va dire 3 (le minimum pour être sûr).
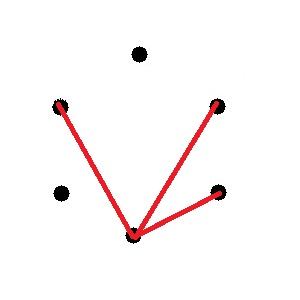
Mais regardes bien, si on prend ces trois points :

Le trait manquant est forcément bleu ! Parce que sinon le triangle serait unicolore, et on ne veut pas que ça arrive !!!
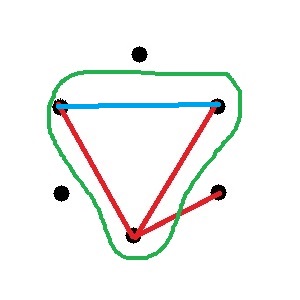
Pareil pour ces trois points là :
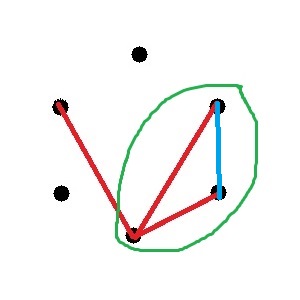
Et pour ceux-ci :
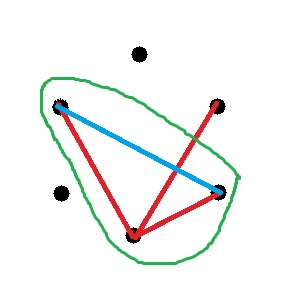
Finalement on a ça :
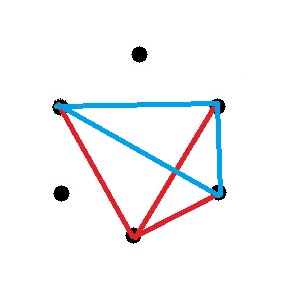
Tu le vois le problème ?
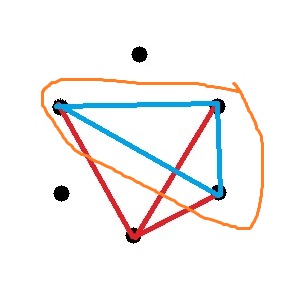
Un Triangle UNICOLORE !!!!
VADE RETRO SATANAS !!!!!
Du coups, si plus de deux arrêtes de la même couleur partent du même sommet, alors le graphe ne peut pas vérifier P3 ... *triste*
Mais en quoi cela pose problème pour le graphe de taille 6 ?
Et bien comptes avec moi, combien d'arêtes partent de chaque sommet ?

Il y a 5 arêtes par sommets ...
Or on a deux couleurs, et sur un sommet chaque couleur ne peut colorier que deux arêtes maximum.
On ne peut pas colorier les cinq arêtes.
Game Over.
C'est bien impossible d'avoir un graphe de taille 6 qui vérifie P3 ...


Mais peut-on colorier le graphe de taille 6 pour qu'il vérifie une nouvelle propriété que nous appellerons P4 ?
Tu l'aura peut-être deviné, P4 est la propriété suivante : Tout sous-graphe de taille 4 n'est pas unicolore.
Je t'invite à y réfléchir pour la prochaine fois où je te montrerais qu'un graphe de taille 6400 peut être colorier pour vérifier P37 XD.
Sur ce, bonne journée/soirée ;-).
Aujourd'hui j'aimerais te parler de coloriage !
Parce que le coloriage, c'est la vie.
Sauf qu'aujourd'hui tu n'auras que 2 couleurs : rouge et bleu.
On va placer plein de points et on va s'amuser à tous les relier entre eux, avec du rouge ou du bleu.
Alors munis-toi d'une feuille et de deux stylos/crayons de couleurs et let's color !!!
Comme ceci par exemple :

On va peut-être prendre plus de points, genre 5.
Et on va les relier entre eux :

Rien de très stimulant intellectuellement, pour l'instant du moins ... ;-)
Alors je te propose un petit casse-tête, quelque chose de simple t'inquiète.
Essaie de relier les 5 points entre eux, en utilisant les deux couleurs, pour qu'aucun triangles ne soit unicolore.
En gros il ne doit pas y avoir de triangles uniquement rouges, ou uniquement bleus.
L'exemple que j'ai donné plus haut ne fonctionne pas, le triangle en bas à droite est complètement rouge.
Ha au fait petit malin, je parle des triangles dont les sommets sont des points noirs, pas des triangles formés par les intersections des traits.
Celui-ci oui :

Celui-ci non :

Si tu n'arrives pas à trouver la réponse, la voici :
- Solution:

Avant d'aller plus loin j'aimerais introduire ici quelques termes.
Non !!! Ne pars pas !!! C'est pas compliqué promis !
Si tu es encore là, déjà merci et bravo, ensuite voici les termes : "Graphes complets".
Qu'est-ce qu'un graphe ? Et bien en math c'est rien de plus que des points et des traits qui relient les points, appelées arêtes.
Il y a une définition plus précise ICI.
Et un graphe complet, et bien c'est juste un graphe où tout les points sont reliés entre eux.
Tu vois que c'était pas dur !
Un petit dernier pour la route : "sous-graphe".
Un sous-graphe d'un graphe G, c'est juste un graphe contenue dans G.
Pas trop mal à la tête ?
Alors pour dire la même chose que plus haut mais avec le bon vocabulaire :
On a un graphe complet de taille 5 (5=le nombre de sommets), appelons-le G (comme Graphe XD vive l'originalité ...)
Et on cherche à colorier chaque arêtes de telle sorte que tout les sous-graphes de taille 3 ne soient pas unicolores.
Prends le temps de digérer cette phrase ;-).
Alors on continue.
Imagine maintenant qu'il y a 6 points à relier.

Et là, même question. Colorie le graphe complet, de taille 6, pour que chaque graphe de taille 3 contenu dedans ne soit pas unicolore.
Ne regarde pas la suite et réfléchis un peu ;-)
Alors ?
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Et bien la solution est simple : il n'y en a pas.
Et oui ce n'est pas possible !
Et je m'en vais te le prouver ! (parce que l'on fais quand même un peu de math XD)
Mais sans faire de calcul ! (parce que l'on fais quand même un peu de dessins XD)
Pour pas se répéter indéfiniment, on dira qu'un graphe G qui peut être colorié (de telle manière à ce que tout sous-graphe de taille 3 ne soit pas unicolore) vérifie la propriété P3.
D'abord, petit Lemme (un lemme c'est un théorème intermédiaire utile pour prouver un autre résultats).
"Si un Graphe vérifie P3, alors de chaque sommets, il ne peut pas partir plus de 2 arêtes de la même couleur."
Alors pourquoi ?
Et bien dessinons.
Si je prends un point et que je trace plus de 2 traits de la même couleur. Plus de 2, donc on va dire 3 (le minimum pour être sûr).

Mais regardes bien, si on prend ces trois points :

Le trait manquant est forcément bleu ! Parce que sinon le triangle serait unicolore, et on ne veut pas que ça arrive !!!

Pareil pour ces trois points là :

Et pour ceux-ci :

Finalement on a ça :

Tu le vois le problème ?

Un Triangle UNICOLORE !!!!
VADE RETRO SATANAS !!!!!
Du coups, si plus de deux arrêtes de la même couleur partent du même sommet, alors le graphe ne peut pas vérifier P3 ... *triste*
Mais en quoi cela pose problème pour le graphe de taille 6 ?
Et bien comptes avec moi, combien d'arêtes partent de chaque sommet ?

Il y a 5 arêtes par sommets ...
Or on a deux couleurs, et sur un sommet chaque couleur ne peut colorier que deux arêtes maximum.
On ne peut pas colorier les cinq arêtes.
Game Over.
C'est bien impossible d'avoir un graphe de taille 6 qui vérifie P3 ...
Mais peut-on colorier le graphe de taille 6 pour qu'il vérifie une nouvelle propriété que nous appellerons P4 ?
Tu l'aura peut-être deviné, P4 est la propriété suivante : Tout sous-graphe de taille 4 n'est pas unicolore.
Je t'invite à y réfléchir pour la prochaine fois où je te montrerais qu'un graphe de taille 6400 peut être colorier pour vérifier P37 XD.
Sur ce, bonne journée/soirée ;-).
Dernière édition par Bacrima le 16.01.17 18:07, édité 2 fois

Bacrima- Humeur : Une pointe de joie et un soupçon d'amusement
Localisation : Dans ma chambre, rarement ailleur ...
Emploi/Loisirs : Japanimer, ça se dit ?
 Re: Let's color
Re: Let's color
Re-coucou lecteur/lectrice.
Prêt(e) pour plus de dessins ?
C'est parti !
On va s’intéresser à P4, tu te rappelles ?
La propriété que peut vérifier un graphe et qui dit que l'on peut le colorier pour qu'aucun sous-graphe de taille 4 ne soit unicolore.
On va se demander si un graphe de taille 6 ou 7 peut vérifier P4.
Je te laisse réfléchir et je cache la solution plus bas.
Et un graphe de taille 8 ?
On ne peut pas utiliser la même astuce ... Car ici on pourrait aisément prendre 4 sommets parmi les 8 qui ne seraient pas voisins sur l'octogone.
Mais si on colorie l'octogone en bleu et que l'on relie en bleu chaque sommet avec le voisin de son voisin (sur l'octogone) ... Son voisin au second degré en quelques sortes.
Cela donne ceci :

Tu vois que si l'on prend 4 points parmi les 8, au moins 2 seront soit voisins, soit voisins au 2nd degré ... Et donc au moins une arête est bleu.
De plus il y aura au moins 2 points qui ne seront ni voisins, ni voisins au 2nd degré. Donc au moins une arrête rouge !
C'est gagné, on a colorié le graphe de taille 8 pour qu'il vérifie P4 !

C'est jolie non ?
Je te laisse te convaincre que cette astuce fonctionne un certain temps, pour tout graphe de taille inférieure à 12 en fait.
Arrivé à 12 on a un petit problème.
Voici le graphe de taille 12 où chaque sommet est relié en bleu avec ses voisins au 1er et 2nd degré, je n'ai volontairement pas dessiné les autres arêtes pour ne pas surcharger le dessin, mais ces autres arrêtes sont rouges.
Regarde les 4 sommets violets.
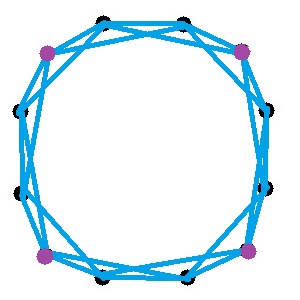
Ce sont 4 sommets qui ne sont pas voisins ni au premier, ni au second degré.
Donc reliés uniquement en rouge.
Donc ils forment un sous-graphe de taille 4 unicolore .... Holly Shit !!!!!!
Mais on ne veut pas ça !!!!!!!!!!
Mince alors ... Tu as une idée pour colorier ce graphe de taille 12 pour qu'il vérifie P4 ?
Peut-être en reliant chaque sommet avec ses voisins au 1er, 2nd et 3ème degré ?
Et bien non, malheureusement si on fait ça, il suffit de prendre 4 points d'affilés sur le dodecagone pour voir qu'ils forment un sous-graphe uniquement bleu.
Pas d'autres idées ?
Et bien moi si ! Essayes de relier chaque sommets opposés par une arrête bleu :-)
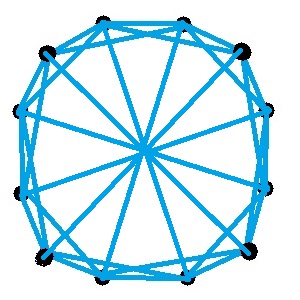
Si tu veux creuser plus loin, pour les graphes de taille 13, 14 ou 15 je t'invite à le faire ;-)
Donnes-moi tes résultats ;-)
Maintenant on va s’intéresser à P5.
On va démontrer P5 pour le graphe de taille 12 ! (En soit c'est déjà fait car on à montré P4 ... Mais c'est juste que la taille 12 est bien pratique pour introduire l'astuce suivante.)
On va maintenant introduire une nouvelle astuce très utile.
On va découpé notre graphe en sous-parties.
Ici en 3 sous-parties de 4 points :

Un avantage de cette manière de dessiner est que l'on va faire des économies de traits.
En effet, on va considérer que chaque point d'un cercle A, et chaque point d'un cercle B, sont reliés entre eux par une arête de même couleur.
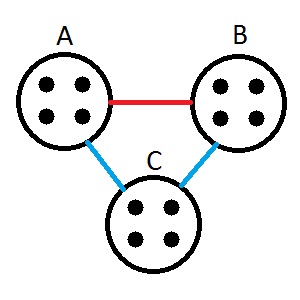
Si tu prends un point de B et un point de C, ils sont reliés entre eux par une arête bleu.
Un point de A et un point de B par une arête rouge.
Mine de rien c'est bien plus lisible car on s'épargne de dessiner 45 arêtes quand même.
Bon, il faut quand même relier les sommets à l'intérieur des cercles.
Je te laisse réfléchir à comment le faire pour vérifier P5 et je te donne la solution plus bas ;-).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Alors ? Tu as trouvé ?
En fait, on va relier les sommets de manière à ce qu'ils vérifient P3.
On va faire de même pour les cercles que l'on relie entre eux pour qu'ils vérifient P3 (c'est pas dur vu qu'il y en a 3 LoL)
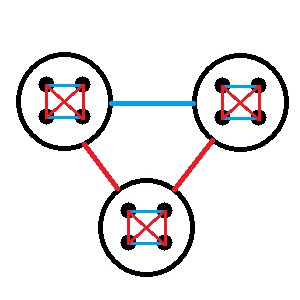
C'est cool non ?
Alors maintenant regarde bien.
Essayons de construire un sous-graphe unicolore de taille 5.
Tout d'abord, remarquons que puisque les sous-graphes des cercles vérifient P3, on ne peut pas prendre plus de deux points dans chaque cercles sans qu'ils ne soient bicolore.
Reformulé autrement : si tu prends 3 points dans le même cercle, tu as un sous-graphe bicolore, car les sous-graphe des cercle vérifient P3.
Donc, maximum 2 points dans le même cercle.
Mais attends un peu, le graphe formé par les trois cercles vérifie aussi P3.
Donc si tu prends des points dans plus de deux cercles différents, c'est mort, tu sera bicolore.
Du coups on peut prendre maximum 2 points dans deux cercles différents pour que ce soit unicolore.
Au-delà le sous-graphe sera bicolore.
Donc il n'y a pas de sous-graphe unicolore de taille 5.
Donc le graphe de taille 12 vérifie P5 !!!!!
Je me suis un peu emporté la dernière fois, lorsque je disais que l'on verrais qu'un graphe de taille 6400 vérifiait P37.
Mais on n'y arrivera, promis ;-)
Sur ce, bonne journée/soirée. ;-)
Prêt(e) pour plus de dessins ?
C'est parti !
On va s’intéresser à P4, tu te rappelles ?
La propriété que peut vérifier un graphe et qui dit que l'on peut le colorier pour qu'aucun sous-graphe de taille 4 ne soit unicolore.
On va se demander si un graphe de taille 6 ou 7 peut vérifier P4.
Je te laisse réfléchir et je cache la solution plus bas.
- Solution:
Pour colorier le graphe on utilise une astuce inspirée de celle utilisée pour que le graphe de taille 5 vérifie P3.
On colorie l'hexagone en bleu, et les autres traits en rouge.
Ainsi si l'on prend 4 sommets parmi les 6, il y en a au moins 2 qui seront voisins sur l'hexagone, et au moins 2 qui ne le seront pas.
On aura donc au moins une arête bleu et une rouge.
Donc pas de sous-graphe de taille 4 unicolore.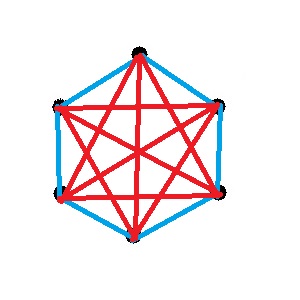
Remarque que cette astuce fonctionne aussi pour un graphe de taille 7, car de même si l'on prends 4 sommets parmi les 7, au moins 2 seront voisins sur l'heptagone, et 2 ne le seront pas :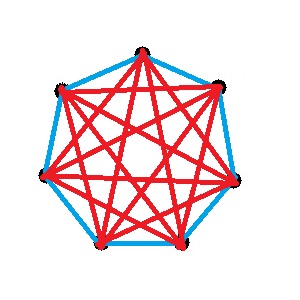
Et un graphe de taille 8 ?
On ne peut pas utiliser la même astuce ... Car ici on pourrait aisément prendre 4 sommets parmi les 8 qui ne seraient pas voisins sur l'octogone.
Mais si on colorie l'octogone en bleu et que l'on relie en bleu chaque sommet avec le voisin de son voisin (sur l'octogone) ... Son voisin au second degré en quelques sortes.
Cela donne ceci :

Tu vois que si l'on prend 4 points parmi les 8, au moins 2 seront soit voisins, soit voisins au 2nd degré ... Et donc au moins une arête est bleu.
De plus il y aura au moins 2 points qui ne seront ni voisins, ni voisins au 2nd degré. Donc au moins une arrête rouge !
C'est gagné, on a colorié le graphe de taille 8 pour qu'il vérifie P4 !

C'est jolie non ?
Je te laisse te convaincre que cette astuce fonctionne un certain temps, pour tout graphe de taille inférieure à 12 en fait.
Arrivé à 12 on a un petit problème.
Voici le graphe de taille 12 où chaque sommet est relié en bleu avec ses voisins au 1er et 2nd degré, je n'ai volontairement pas dessiné les autres arêtes pour ne pas surcharger le dessin, mais ces autres arrêtes sont rouges.
Regarde les 4 sommets violets.

Ce sont 4 sommets qui ne sont pas voisins ni au premier, ni au second degré.
Donc reliés uniquement en rouge.
Donc ils forment un sous-graphe de taille 4 unicolore .... Holly Shit !!!!!!
Mais on ne veut pas ça !!!!!!!!!!
Mince alors ... Tu as une idée pour colorier ce graphe de taille 12 pour qu'il vérifie P4 ?
Peut-être en reliant chaque sommet avec ses voisins au 1er, 2nd et 3ème degré ?
Et bien non, malheureusement si on fait ça, il suffit de prendre 4 points d'affilés sur le dodecagone pour voir qu'ils forment un sous-graphe uniquement bleu.
Pas d'autres idées ?
Et bien moi si ! Essayes de relier chaque sommets opposés par une arrête bleu :-)

Si tu veux creuser plus loin, pour les graphes de taille 13, 14 ou 15 je t'invite à le faire ;-)
Donnes-moi tes résultats ;-)
Maintenant on va s’intéresser à P5.
On va démontrer P5 pour le graphe de taille 12 ! (En soit c'est déjà fait car on à montré P4 ... Mais c'est juste que la taille 12 est bien pratique pour introduire l'astuce suivante.)
On va maintenant introduire une nouvelle astuce très utile.
On va découpé notre graphe en sous-parties.
Ici en 3 sous-parties de 4 points :

Un avantage de cette manière de dessiner est que l'on va faire des économies de traits.
En effet, on va considérer que chaque point d'un cercle A, et chaque point d'un cercle B, sont reliés entre eux par une arête de même couleur.

Si tu prends un point de B et un point de C, ils sont reliés entre eux par une arête bleu.
Un point de A et un point de B par une arête rouge.
Mine de rien c'est bien plus lisible car on s'épargne de dessiner 45 arêtes quand même.
Bon, il faut quand même relier les sommets à l'intérieur des cercles.
Je te laisse réfléchir à comment le faire pour vérifier P5 et je te donne la solution plus bas ;-).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Alors ? Tu as trouvé ?
En fait, on va relier les sommets de manière à ce qu'ils vérifient P3.
On va faire de même pour les cercles que l'on relie entre eux pour qu'ils vérifient P3 (c'est pas dur vu qu'il y en a 3 LoL)

C'est cool non ?
Alors maintenant regarde bien.
Essayons de construire un sous-graphe unicolore de taille 5.
Tout d'abord, remarquons que puisque les sous-graphes des cercles vérifient P3, on ne peut pas prendre plus de deux points dans chaque cercles sans qu'ils ne soient bicolore.
Reformulé autrement : si tu prends 3 points dans le même cercle, tu as un sous-graphe bicolore, car les sous-graphe des cercle vérifient P3.
Donc, maximum 2 points dans le même cercle.
Mais attends un peu, le graphe formé par les trois cercles vérifie aussi P3.
Donc si tu prends des points dans plus de deux cercles différents, c'est mort, tu sera bicolore.
Du coups on peut prendre maximum 2 points dans deux cercles différents pour que ce soit unicolore.
Au-delà le sous-graphe sera bicolore.
Donc il n'y a pas de sous-graphe unicolore de taille 5.
Donc le graphe de taille 12 vérifie P5 !!!!!
Je me suis un peu emporté la dernière fois, lorsque je disais que l'on verrais qu'un graphe de taille 6400 vérifiait P37.
Mais on n'y arrivera, promis ;-)
Sur ce, bonne journée/soirée. ;-)
Dernière édition par Bacrima le 28.08.17 23:53, édité 1 fois

Bacrima- Humeur : Une pointe de joie et un soupçon d'amusement
Localisation : Dans ma chambre, rarement ailleur ...
Emploi/Loisirs : Japanimer, ça se dit ?
 Re: Let's color
Re: Let's color
Pas mal du tout !
J'ai mis le temps à lire (en fait, j'ai dû relire deux fois pour ne pas me perdre (chaque fois j'inversais à un moment en confondant Pn et ¬Pn)) mais ça a fini par être clair. ^^
Ça provient d'où par curiosité ?
J'ai mis le temps à lire (en fait, j'ai dû relire deux fois pour ne pas me perdre (chaque fois j'inversais à un moment en confondant Pn et ¬Pn)) mais ça a fini par être clair. ^^
Ça provient d'où par curiosité ?

Yoendel- Humeur : variable... dérivable... et même C-infinie
 Re: Let's color
Re: Let's color
Une vidéo youtube en a parlé vite fait et je suis tombé amoureuse du problème ^^

Bacrima- Humeur : Une pointe de joie et un soupçon d'amusement
Localisation : Dans ma chambre, rarement ailleur ...
Emploi/Loisirs : Japanimer, ça se dit ?
 Re: Let's color
Re: Let's color
Coucou lecteurice !
Me revoilà 2 ans et demi plus tard pour terminer ce post ^^.
Alors donc, comme on l'a vu la dernière fois, on peut découper un graphe en sous-graphe que l'on met dans des "cercles" pour faciliter le coloriage.
Dans l'exemple précédent le graphe complet de taille 12 a été découpé en 3 sous-graphes de taille 4.
(Remarque que l'on aurait pu aussi découper ce graphe en 4 sous-graphes de taille 3.)
L'important ici c'est que les sous-graphes de taille 3 et 4 étaient colorier pour vérifier tout les deux P3.
Donc on pouvait "prendre" au maximum 2 sommets dans 2 cercles différents sans former obligatoirement un sous-graphe bicolore.
Ce qui nous permettait de conclure qu'un sous-graphe de taille (2*2+1) 5 était, lui, forcément bicolore.
Imaginons un graphe complet de taille 144. (oui, c'est énorme)
On peut le 'découper' en 12 sous-graphes de taille 12.
On a montré que le graphe de taille 12 vérifiait P4, donc on aura forcément un sous-graphe bicolore si on prends plus que 3 sommets dans 3 cercles différents, soit 3x3+1 = 10 sommets.
Donc le graphe de taille 144 vérifie P10, et on a même la façon de le colorier !
Ce que l'on voit c'est que si on a un graphe de taille AxB, que A vérifie Pn et B vérifie Pm alors le graphe de taille AxB vérifie Pu où u =(n-1)x(m-1)+1
Me revoilà 2 ans et demi plus tard pour terminer ce post ^^.
Alors donc, comme on l'a vu la dernière fois, on peut découper un graphe en sous-graphe que l'on met dans des "cercles" pour faciliter le coloriage.
Dans l'exemple précédent le graphe complet de taille 12 a été découpé en 3 sous-graphes de taille 4.
(Remarque que l'on aurait pu aussi découper ce graphe en 4 sous-graphes de taille 3.)
L'important ici c'est que les sous-graphes de taille 3 et 4 étaient colorier pour vérifier tout les deux P3.
Donc on pouvait "prendre" au maximum 2 sommets dans 2 cercles différents sans former obligatoirement un sous-graphe bicolore.
Ce qui nous permettait de conclure qu'un sous-graphe de taille (2*2+1) 5 était, lui, forcément bicolore.
Imaginons un graphe complet de taille 144. (oui, c'est énorme)
On peut le 'découper' en 12 sous-graphes de taille 12.
On a montré que le graphe de taille 12 vérifiait P4, donc on aura forcément un sous-graphe bicolore si on prends plus que 3 sommets dans 3 cercles différents, soit 3x3+1 = 10 sommets.
Donc le graphe de taille 144 vérifie P10, et on a même la façon de le colorier !
Ce que l'on voit c'est que si on a un graphe de taille AxB, que A vérifie Pn et B vérifie Pm alors le graphe de taille AxB vérifie Pu où u =(n-1)x(m-1)+1

Bacrima- Humeur : Une pointe de joie et un soupçon d'amusement
Localisation : Dans ma chambre, rarement ailleur ...
Emploi/Loisirs : Japanimer, ça se dit ?
 Re: Let's color
Re: Let's color
On peut même montrer que si un graphe est de taille A1xA2xA3x.....xAn et que A1,A2,A3, ... ,An vérifient respectivement Pa1,Pa2, ..., Pan, alors le graphe de taille A1xA2xA3x.....xAn verifie Pu où u=(a1-1)x(a2-1)x...x(an-1)+1

Bacrima- Humeur : Une pointe de joie et un soupçon d'amusement
Localisation : Dans ma chambre, rarement ailleur ...
Emploi/Loisirs : Japanimer, ça se dit ?
Page 1 sur 1
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum|
|
|
